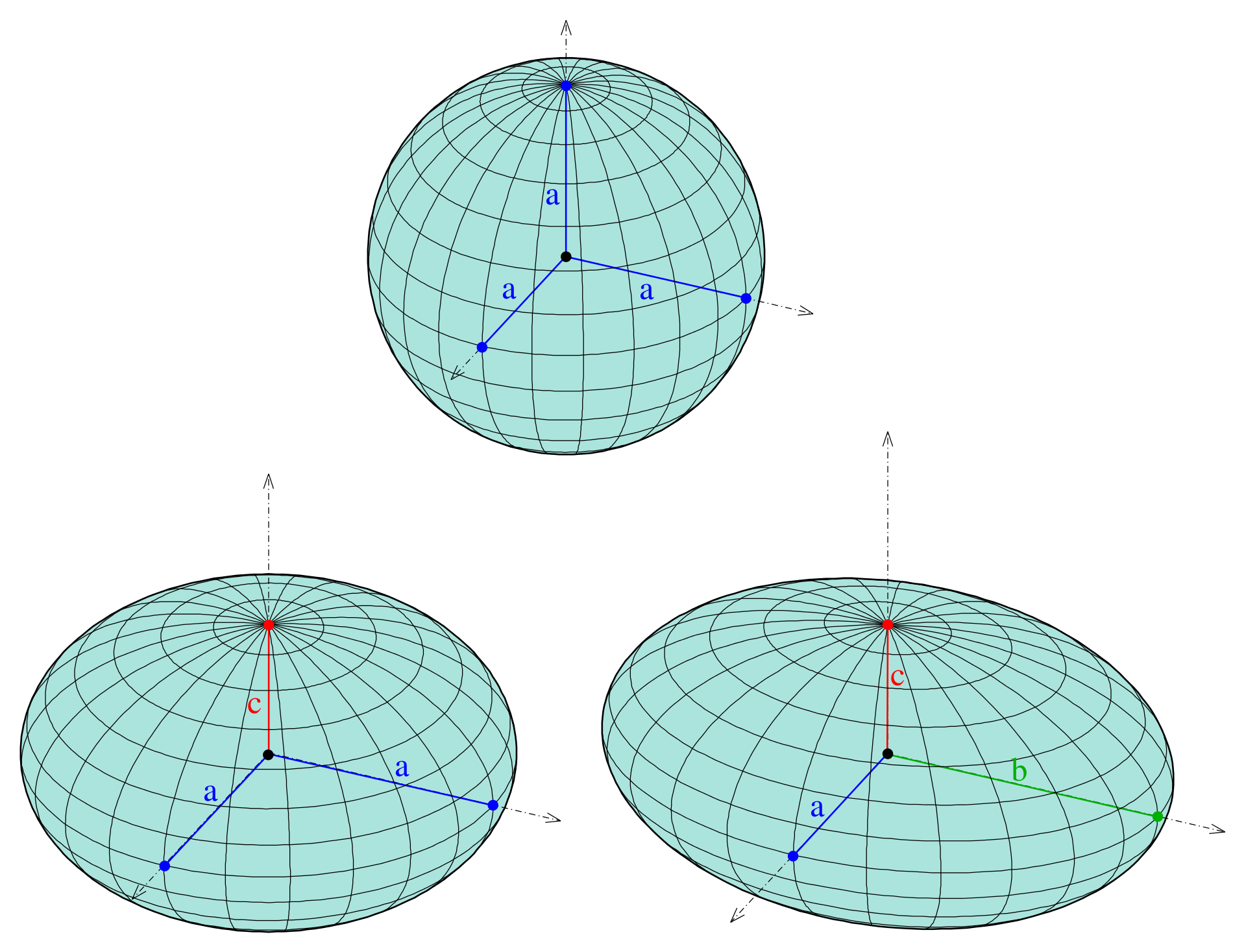
椭球
在三维直角坐标系中的表示方式为: \(\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}=1\) 其中$a$和$b$是赤道半径(沿着$x$和$y$轴),$c$是极半径(沿着$z$轴),它们共同决定类椭球的形状。当$a=b=c$时,即为球。如果有两个半径是相等的,则是一个类球面。 大地测量中,用于描述地球形状参考椭球便是一个类球面($a=b>c$)。
在球坐标系中, \(X = a\,sin(\theta)cos(\varphi);\\ Y = b\,sin(\theta)sin(\varphi);\\ Z = c\,cos(\theta);\)
其中 $\theta\in[0,180]$ 是天顶角,$\varphi \in [0,360]$是方位角。
参考椭球
在大地测量学中, 参考椭球是一个数学上定义的地球表面,它近似于大地水准面。 由于其相对简单,参考椭球是大地控制网计算和显示点坐标(如纬度,经度和海拔)的首选的地球表面的几何模型。通常所说地球的形状和大小,实际上就是以参考椭球的长半轴、短半轴和扁率来表示的。
分别用$a$,$b$表示参考椭球的长半轴和短半轴,参考椭球可以用下式表示: \(\frac{x^2+y^2}{a}+\frac{z^2}{b}=1\) 参考椭球的具有以下5个基本几何元素:
- 长半轴:$a$
- 短半轴:$b$
- 扁率: \(\alpha = \frac{a-b}{a}\)
- 第一偏心率: \(e = \frac{\sqrt{a^2-b^2}}{a}\)
- 第二偏心率: \(e' = \frac{\sqrt{a^2-b^2}}{b}\)
其中,$a$、$b$是长度元素,另外三个参数则反映了参考椭球的扁平程度。五个元素中只需有一个长度元素与其他任意参数即可确定参考椭球的形状、大小,如$a$和$e$。
几个常用椭球参数如下,其中克拉索夫斯基椭球是北京54坐标系采用的参考椭球、IUGG1975椭球是西安80坐标系采用的参考椭球、国家2000坐标系(CGCS2000)则基本采用IUGG1980椭球参数:
| 椭球 | $a(m)$ | $b(m)$ | $\alpha$ | $e^2$ | $e’^2$ |
|---|---|---|---|---|---|
| 克拉索夫斯基椭球 | 6378245.0000 | 6356863.0188 | 1:298.3 | 0.006693421622966 | 0.006738525414683 |
| IUGG1975椭球 | 6378140.0000 | 6356755.2882 | 1:298.257 | 0.006694384999588 | 0.006739501819473 |
| IUGG1980椭球 | 6378137.0000 | 6356752.3141 | 1:298.257222101 | 0.00669438002290 | 0.00673949677548 |
在近似估算时,可取以下值: \(a\approx b \approx 6400 km \\ \alpha \approx 1:300 \\ e^2\approx e'^2 \approx 1:150 \approx 0.0007\)
大地坐标与直角坐标系
为了能够表示椭球上的点位置,需要建立合适的坐标系,常用的坐标系有空间直角坐标系和大地坐标系。使用它们能够表示椭球上的任意点的位置,二者直接也可以进行精确转换。
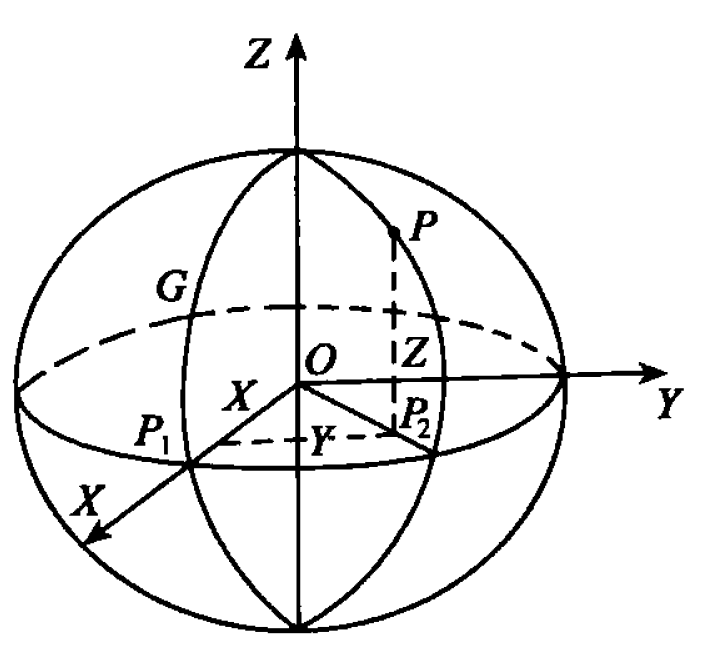
空间直角坐标系
如图,以椭球中心O为原点,起始子午面与赤道面交线为X轴,在赤道面上与X轴正交的方法为Y轴,椭球体的旋转轴为Z轴,构成右手坐标系O-XYZ,P点则可以用(x,y,z)表示。
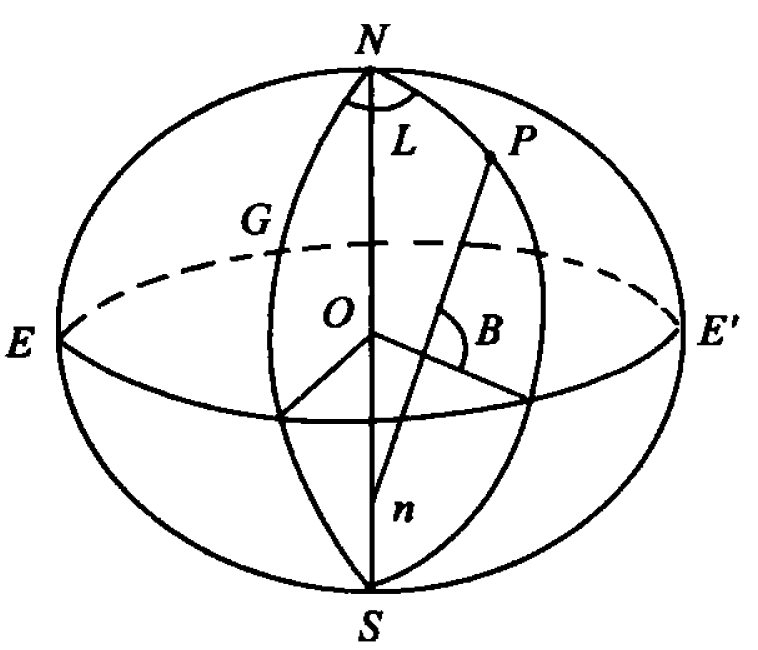
大地坐标
大地坐标由经纬度与大地高组成。经度由起始子午面起算,向东为正,叫东经(0°~180°);向西为负,叫西经(0°~180°)。纬度由赤道面起算,向北为正,叫北纬(0°~90°);向南为负,叫南纬(0°~90°)。大地高是一点沿椭球法线到椭球面的距离,对于椭球面上的点$H=0$。在该坐标系中,P点的位置可用(L,B,0)表示。
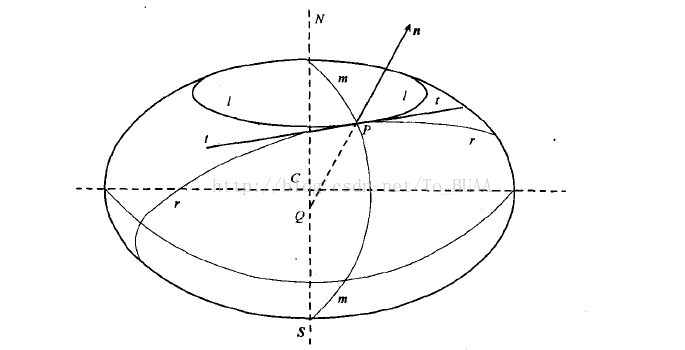
子午圈和卯酉圈及其曲率半径
过球面上任意一点可作一条垂直于球面的法线,包含这条法线的平面叫做法截面,法截面同球面交线叫法截线(或法截弧)。过球面上一点的法线,可以做无数个 多个法截面,即有无数个法截线。其中有两个特殊的法截线——子午圈和卯酉圈。在椭球上,这两个法截线的曲率半径是不相同的。
子午圈
子午圈,是指同时过椭球旋转轴与地面点法线的法截面(子午面)与椭球的交线,即图中mPm,也称经圈,其与点所在经度线平行。子午圈曲率半径的计算公式为: \(M = \frac{a(1-e^2)}{(1-e^2sin^2(B))^{\frac{3}{2}}}\) 卯酉圈
过椭球面上一点的法线所作的法截面中,与子午面相垂直的法截面与椭球交线称为卯酉圈,及图中rPr。其曲率半径为: \(N = \frac{a}{\sqrt{1-e^2sin^2(B)}}\)
坐标转换
上述大地坐标系与空间直角坐标系的表示形式、数值之间存在差异,但由于是表示相同点的位置,那么它们之间必然存在联系。类比球坐标与直角坐标之间的关系及椭球的性质,我们可以得到由大地坐标系(L,B,H)向空间直角坐标系(X,Y,Z)的转换方法: \(X = N\,cos(B)cos(L);\\ Y = N\,cos(B)sin(L);\\ Z = N(1-e^2)\,sin(B);\) 那么,由空间直角坐标系(X,Y,Z)向大地坐标系(L,B,H)转换方法则是: \(L = arctan(\frac{Y}{X})\\ tan(B) = \frac{Z+N\cdot e^2sin(B)}{\sqrt{X^2+Y^2}}\\ H = \frac{\sqrt{X^2+Y^2}}{cos{B}}-N\)
上式中,纬度$B$与大地高$H$可以进行迭代计算得到,其中纬度的初值$B_0$可以取 \(B_0 = arctan(\frac{Z}{\sqrt{X^2+Y^2}})\)
当两次计算的$B$值的绝对值之差小于0.0001”即可。
坐标转换示例
下面是按照上面方法编写的C++坐标转换程序的部分代码:
#define PI 3.14159265358979323846
#define DEG2RAD PI/180
#define RAD2DEG 180/PI
class COORD3 {
public:
double p1,p2,p3;
COORD3(double a1=0,double b1=0,double c1=0){
this->p1=a1;
this->p2=b1;
this->p3=c1;
};
};
// 大地坐标转换为空间直角坐标
COORD3 lbh2xyz(double l,double b,double h, double a, double e){
double N; // 卯酉圈曲率半径
COORD3 xyz(0,0,0);
l = l*DEG2RAD; //转为弧度
b = b*DEG2RAD;
N = a/sqrt(1.0-e*e*sin(b)*sin(b));
xyz.p1 = (N+h)*cos(b)*cos(l); // X
xyz.p2 = (N+h)*cos(b)*sin(l); // Y
xyz.p3 = (N*(1-e*e)+h)*sin(b); // Z
return xyz;
};
// 空间直角坐标转换为大地坐标
COORD3 xyz2lbh(double x,double y,double z, double a, double e){
double b0,b,N,R;
double err;
COORD3 lbh;
R = sqrt(x*x+y*y);
b0 = atan2(z,R);
do{
N = a/sqrt(1.0-e*e*sin(b0)*sin(b0));
b = atan2(z+N*e*e*sin(b0),R);
err = b-b0;
b0 = b;
}while (fabs(err)>0.0001/3600*DEG2RAD);
lbh.p2 = b*RAD2DEG; // B
lbh.p1 = atan2(y,x)*RAD2DEG; // L
lbh.p3 = R/cos(b)-N; //H
return lbh;
};
使用不同椭球参数的转换结果:
1、由大地坐标转换为空间直角坐标:$L=77^{\circ}11’22.333^”, B=33^{\circ}44’55.666^”, H=5555.66m$
| 参考椭球 | X/m | Y/m | Z/m |
|---|---|---|---|
| 克拉索夫斯基椭球 | 1178143.531589 | 5181238.389636 | 3526461.538191 |
| IUGG1975椭球 | 1178124.328965 | 5181153.940356 | 3526400.643389 |
| IUGG1980椭球 | 1178123.774402 | 5181151.501501 | 3526399.001116 |
2、由空间直角坐标转换为大地坐标:$X=1177888.777m, Y=5166777.888m, Z=3544555.666m$
| 参考椭球 | L | B | H/m |
|---|---|---|---|
| 克拉索夫斯基椭球 | 77°09’27.204862” | 33°57’18.748384” | 3878.534084 |
| IUGG1975椭球 | 77°09’27.204862” | 33°57’18.830340” | 3984.383865 |
| IUGG1980椭球 | 77°09’27.204862” | 33°57’18.829560” | 3987.375774 |
参考
- 椭球 - 维基百科,自由的百科全书
- 参考椭球 - 维基百科,自由的百科全书
- 子午圈 - 维基百科,自由的百科全书
- 卯酉圈 - 维基百科,自由的百科全书
- 大地坐标系与空间直角坐标系的转换 - 知乎
- 大地测量学基础-吕志平、乔书波
- 大地测量学基础-孔祥元、郭际明