平面直角坐标系及三维直角坐标系变换公式推导。
坐标系的变换一般有旋转、平移、缩放等多种。其中平移、缩放比较容易理解,例如二维直角坐标系中有一点A的坐标$(x_A,y_A)$,若将坐标系沿$X$轴平移$m$,沿$Y$轴平移$n$,那么A点的新坐标值$(x_A’, y_A’)$为:
\[\begin{matrix} \left[\begin{matrix} x_A' \\ y_A' \\ 1 \end{matrix}\right] = \left[\begin{matrix} 1 & 0 & m \\ 0 & 1 & n \\ 0 & 0 & 1 \end{matrix}\right]\left[\begin{matrix} x_A \\ y_A \\ 1 \end{matrix}\right] \end{matrix}\]若再将坐标系分别沿$X$轴、$Y$轴缩放$j$、$j$倍,那么此时A的坐标值$(x_A’’, y_A’’)$为:
\[\begin{matrix} \left[\begin{matrix} x_A'' \\ y_A'' \\ 1 \\ \end{matrix}\right] &=& \left[\begin{matrix} i & 0 & 0 \\ 0 & j & 0 \\ 0 & 0 & 1 \end{matrix}\right]\left[\begin{matrix} x_A' \\ y_A' \\ 1 \end{matrix}\right] \\ \\ &=& \left[\begin{matrix} i \cdot (m + x_A) \\ j \cdot (n + y_A) \\ 1 \end{matrix}\right] \end{matrix}\]坐标系的旋转相对复杂一些,下面将从二维坐标系入手,逐步推导出二维直角坐标系和三维直角坐标系的旋转计算方法。
二维直角坐标系旋转
文中论述坐标系采用右手系,且定义顺时针旋转为正方向,下面使用两种方法来推导坐标系旋转计算公式。
二维坐标旋转推导方法1
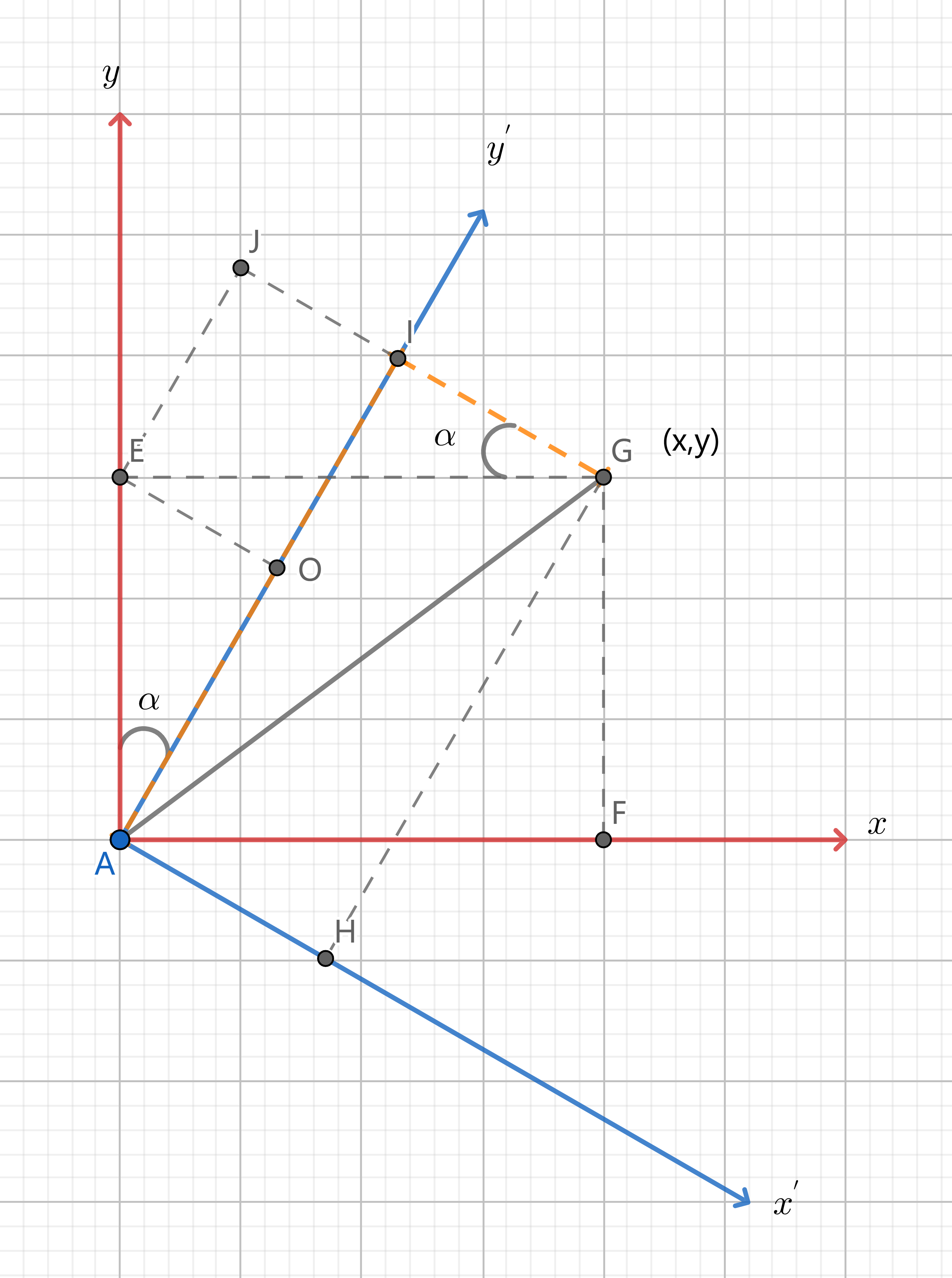
如下图所示,G点在坐标系$O-XY$中的坐标为$(x,y)$,坐标系$A-X’Y’$由源坐标系顺时针旋转$\alpha$角度得到,需要计算G点在$A-X’Y’$中的坐标值$(x’,y’)$。图中E、F点分别是G点在y轴,x轴上的投影,I、H点是G点在y’轴、x’轴上的投影。过E点做y’轴的垂线,交于O点,过E点做y’轴平行线,交GI延迟线于J点。从图中可以看出:
\[\begin{matrix} x' = L_{GJ} - L_{IJ} \\ y' = L_{AO} + L_{OI} \end{matrix}\]由于$\angle EGJ = \alpha$,$L_{EG}=x$,在$\triangle GEJ$中有:
\(L_{GJ} = x\cos(\alpha) \\ L_{EJ} = x\sin(\alpha)\) 在$\triangle AOE$中有:
\[L_{AO} = y\cos(\alpha) \\ L_{OE} = y\sin(\alpha)\]同时在矩形$OIJE$中有:
\(L_{IJ} = L_{OE}\\ L_{OI} = L_{EJ}\),因此有:
\[x' = x\cos(\alpha) - y \sin(\alpha)\\ y' = y\cos(\alpha) + x \sin(\alpha)\]二维坐标旋转推导方法2
坐标系与其中的参考点是相对的关系,前面的分析方法中保持参考点不动,坐标旋转顺时针$\alpha$角度。那么如果假设坐标系不动,考察旋转变换后的参考点向量,相当于相对源向量逆时针旋转$\alpha$角度。
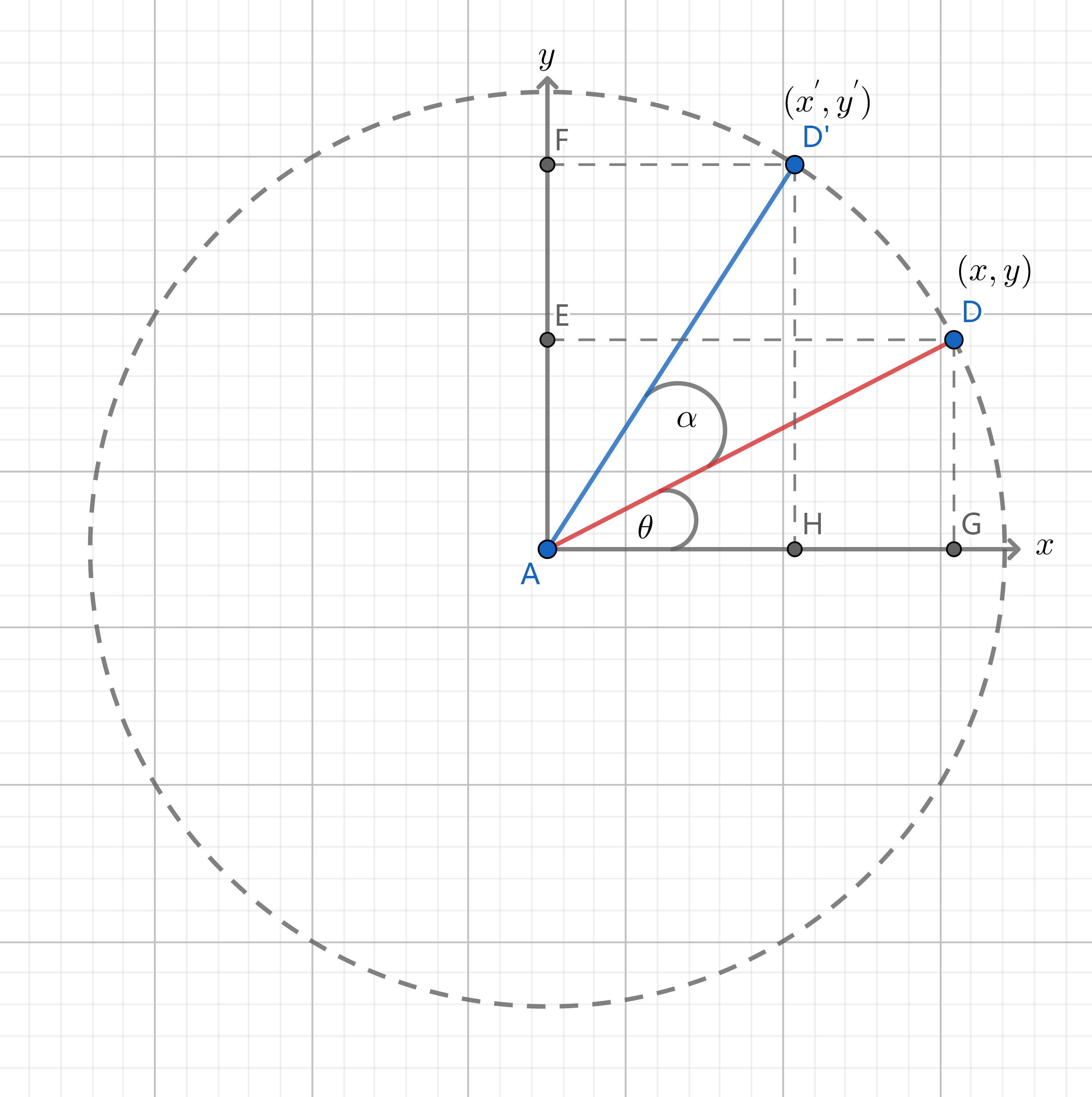
下图中假设向量$\overrightarrow{AD}$长度为$r$,坐标值为$(x, y)$,向量$\overrightarrow{AD’}$是由向量$\overrightarrow{AD}$逆时针旋转$\alpha$角度得到,从图中可以得到如下关系:
\[x = r\cos(\theta) \\ y = r\sin(\theta) \\\] \[x' = r\cos(\theta+\alpha) = r\cos(\theta)\cos(\alpha) - r\sin(\theta)\sin(\alpha)\\ y' = r\sin(\theta+\alpha) = r\sin(\theta)\cos(\alpha) - r\cos(\theta)\sin(\alpha)\]将$x$,$y$的值带入有:
\[x' = x\cos(\alpha) - y \sin(\alpha)\\ y' = y\cos(\alpha) + x \sin(\alpha)\]上述$(x,y)$与$(x’,y’)$的变换关系可以写成矩阵的形式
\[\begin{matrix} \left[\begin{matrix} x' \\ y' \end{matrix}\right] &=& \left[\begin{matrix} \cos(\alpha) & -\sin(\alpha) \\ \sin(\alpha) & \cos(\alpha) \end{matrix}\right] \left[\begin{matrix} x \\ y \end{matrix}\right] \\ & = & R(\alpha) \left[\begin{matrix} x \\ y \end{matrix}\right] \end{matrix}\]其中$R(\alpha)$称为旋转矩阵,旋转角$\alpha$也称为欧拉角。
三维直角坐标系旋转
三维直角坐标系的旋转有三个自由度,可以分别拆分为绕X轴旋转、绕Y轴旋转、绕Z轴旋转,各自可分别视为二维坐标系的旋转,转换公式与二维相似。
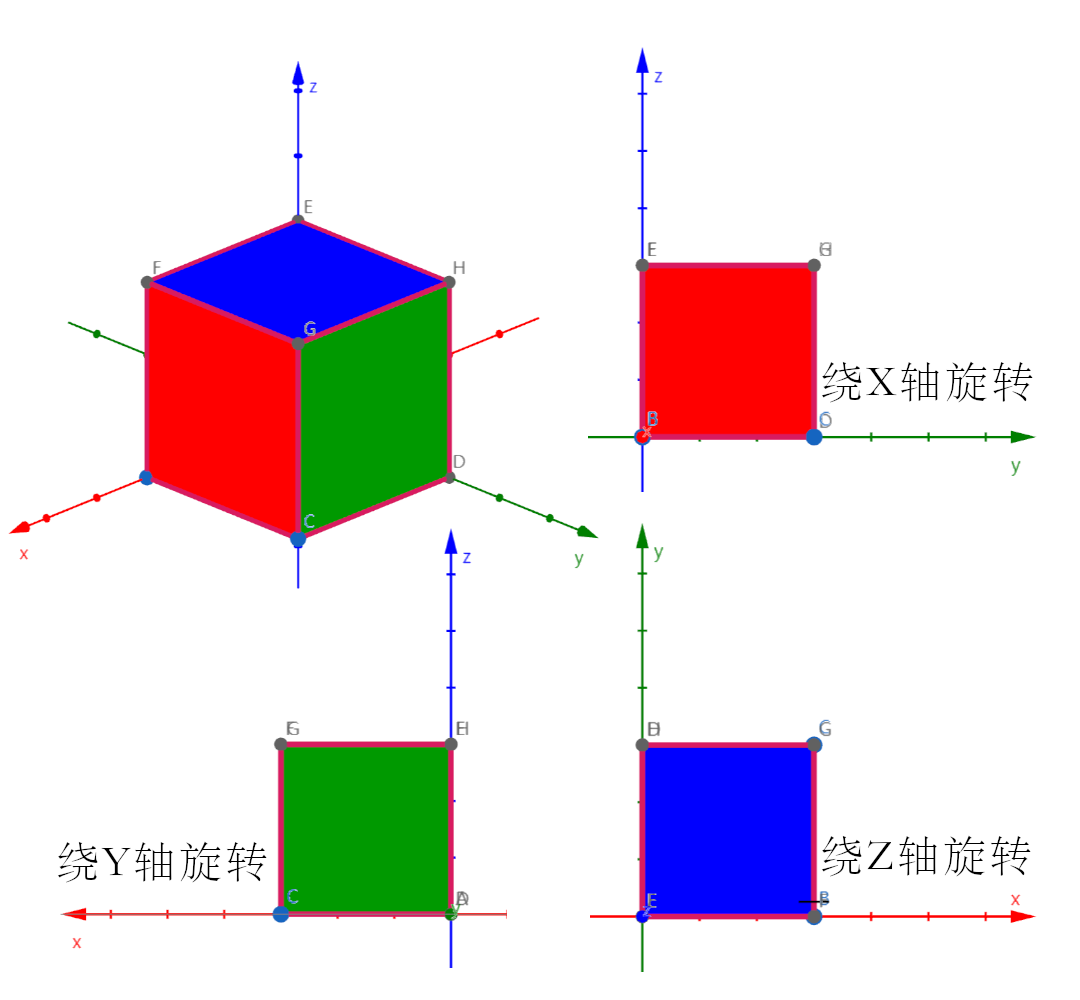
首先需要明确绕X轴、绕Y轴和绕Z轴的旋转方向定义是一致,与二维坐标系分析相同右手系,顺时针旋转为正。结合下图分析,图中左上角是立体图,从X轴、Y轴、Z轴的正方向观察可以分别看到立方体的三面颜色分别为红(右上)、绿(左下)、蓝(右下)。从图中可以看出,绕Y轴旋转时的平面坐标与另外两个为轴对称关系,与我们前面二维坐标变换分析中的使用的坐标系不同。分别列出三种旋转中三维系的的平面坐标轴与二维坐标轴的映射关系
三维直角坐标系XYZ中,绕X轴旋转时YZ轴与二维坐标轴的映射关系 \(Z \Rightarrow Y \\ Y \Rightarrow X\)
绕Y轴旋转时XZ轴与二维坐标轴的映射关系 \(X \Rightarrow Y \\ Z \Rightarrow X\)
绕Z轴旋转时XY轴与二维坐标轴的映射关系 \(Y \Rightarrow Y \\ X \Rightarrow X\)
零绕X轴、Y轴、Z轴旋转角分别为 $\epsilon_x$、$\epsilon_y$、$\epsilon_z$ 将上述映射关系带入到二维旋转矩阵中有:
- 绕X轴旋转 \(\begin{matrix} \left[\begin{matrix} y' \\ z' \end{matrix}\right] &=& \left[\begin{matrix} \cos(\epsilon_x) & -\sin(\epsilon_x) \\ \sin(\epsilon_x) & \cos(\epsilon_x) \end{matrix}\right] \left[\begin{matrix} y \\ z \end{matrix}\right] \end{matrix}\)
- 绕Y轴旋转 \(\begin{matrix} \left[\begin{matrix} z' \\ x' \end{matrix}\right] &=& \left[\begin{matrix} \cos(\epsilon_y) & -\sin(\epsilon_y) \\ \sin(\epsilon_y) & \cos(\epsilon_y) \end{matrix}\right] \left[\begin{matrix} z \\ x \end{matrix}\right] \end{matrix}\)
- 绕Z轴旋转 \(\begin{matrix} \left[\begin{matrix} x' \\ y' \end{matrix}\right] &=& \left[\begin{matrix} \cos(\epsilon_z) & -\sin(\epsilon_z) \\ \sin(\epsilon_z) & \cos(\epsilon_z) \end{matrix}\right] \left[\begin{matrix} x \\ y \end{matrix}\right] \end{matrix}\)
分别扩展到三维后有如下关系:
- 绕X轴旋转 \(\begin{matrix} \left[\begin{matrix} x' \\ y' \\ z' \end{matrix}\right] &=& \left[\begin{matrix} 1 & 0 & 0 \\ 0 & \cos(\epsilon_x) & -\sin(\epsilon_x) \\ 0 & \sin(\epsilon_x) & \cos(\epsilon_x) \end{matrix}\right] \left[\begin{matrix} x \\ y \\ z \end{matrix}\right] \end{matrix}\)
- 绕Y轴旋转 \(\begin{matrix} \left[\begin{matrix} y' \\ z' \\ x' \end{matrix}\right] &=& \left[\begin{matrix} 1 & 0 & 0 \\ 0 & \cos(\epsilon_y) & -\sin(\epsilon_y) \\ 0 & \sin(\epsilon_y) & \cos(\epsilon_y) \end{matrix}\right] \left[\begin{matrix} y \\ z \\ x \end{matrix}\right] \end{matrix}\)
- 绕Z轴旋转 \(\begin{matrix} \left[\begin{matrix} x' \\ y' \\ z' \end{matrix}\right] &=& \left[\begin{matrix} \cos(\epsilon_z) & -\sin(\epsilon_z) & 0\\ \sin(\epsilon_z) & \cos(\epsilon_z) & 0 \\ 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} x \\ y \\ z \end{matrix}\right] \end{matrix}\)
其中绕Y轴旋转时坐标轴映射顺序与另外两个相相反,将其旋转公式展开: \(\begin{matrix} x' = x\cos(\alpha) + 0y + z\sin(\alpha) \\ y' = 0x + 1y + 0z \\ z' = -x\sin(\alpha) + 0y + z\cos(\alpha) \\ \end{matrix}\)
并重新整理后有:
\[\begin{matrix} \begin{bmatrix} x' \\ y'\\ z' \end{bmatrix} = \begin{bmatrix} \cos(\alpha) & 0 & \sin(\alpha) \\ 0 & 1 & 0 \\ -\sin(\alpha) & 0 & \cos(\alpha) \end{bmatrix} \end{matrix}\]由此可以得到三维坐标系中绕X轴、Y轴、Z轴的旋转矩阵为:,那么其旋转矩阵 $R(\epsilon_x)$、$R(\epsilon_y)$、$R(\epsilon_z)$ 分别为:
\(R(\epsilon_x) = \begin{bmatrix} 1 & 0 & 0\\ 0 & \cos(\epsilon_z)& -\sin(\epsilon_z) \\ 0 & \sin(\epsilon_z)& \cos(\epsilon_z) \\ \end{bmatrix}\) \(R(\epsilon_y) = \begin{bmatrix} \cos(\epsilon_z)& 0 & \sin(\epsilon_z) \\ 0 & 1 & 0 \\ -\sin(\epsilon_z)& 0 & \cos(\epsilon_z) \end{bmatrix}\) \(R(\epsilon_z) = \begin{bmatrix} \cos(\epsilon_z)& -\sin(\epsilon_z)& 0 \\ \sin(\epsilon_z)& \cos(\epsilon_z)& 0 \\ 0 & 0 & 1 \end{bmatrix}\)
若将三维直角坐标系O-XYZ分别绕Z轴旋转 $\epsilon_z$、绕Y轴旋转 $\epsilon_y$、绕X轴旋转 $\epsilon_x$,得到O-X’Y’Z’,则有如下转换关系
\[\begin{bmatrix}x' \\ y' \\ z' \end{bmatrix} = R(\epsilon_x)R(\epsilon_y)R(\epsilon_z) \begin{bmatrix}x \\ y \\ z \end{bmatrix}\]