对机器学习中的线性回归和逻辑回归的梯度下降算法知识点总结,包括假设函数、代价函数、梯度下降算法及实行,文中同时也介绍了线性回归的正规方程解法、两种回归的梯度下降算法的差异。
符号约定:
$m$ - 训练集中样本数量
$n$ - 样本的特征数量
$x$ - 输入变量
$\theta$ - 回归系数(预测参数)
$y$ - 目标变量
$x_i^j$ - 第$j$个样本中的第$i$个变量
线性回归
线性回归可发现输入变量与目标变量之间的相关关系,从而根据已知的条件来预测结果。
假设函数(hypothesis Fun)
\(h_{\theta}(x)=\theta_0+\theta_1x_1+...+\theta_nx_n = \sum_{i=0}^n\theta_ix_i=\theta^Tx\)
式中,$x_0$=1。
代价函数(Cost Fun)
\(J(\theta) = \frac{1}{2m}\sum_{j=1}^m(h_{\theta}(x^i)-y^j)^2\)
代价函数反映了在给定预测参数$\theta$下,假设函数与实际结果的差距,为了能够得到最优的拟合结果,我们需要找到最佳拟合参数$\theta$使得代价函数最小。
求解最优参数的方法:梯度下降法,正规方程
梯度下降法 开始时我们随机选择一个参数的组合$(\theta_0,\theta_1,…,\theta_n)$,计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值(local minimum)。
批量梯度下降 (BGD, batch gradient descent) 的算法:
\[\begin{align} repeat :&\\ &\theta_j := \theta_j-\alpha\frac{\partial}{\partial{\theta_j}}{J(\theta)},\ (j=0,1,...,m)\\ \end{align}\]其中,$\frac{\partial}{\partial{\theta_j}}{J(\theta)} = \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^i)-y^i)x_j^i$,我们开始随机选择一组的参数,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛,方可得到最优的参数$\theta$。
正规方程( Normal Equation) 假设函数:$h_{\theta}(X)=X\theta$,代价函数:$J(\theta)=\frac{1}{2}(h_{\theta}(X)-y)^T(h_{\theta}(X)-y)$ 其中,
\[\begin{align} X=&\begin{bmatrix} 1 & x_1^1 & \cdots & x_n^1 \\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_1^m & \cdots & x_n^m \end{bmatrix}(size:m*(n+1)),\\ \theta=& \begin{bmatrix}\theta_0 \\ \theta_1\\ \vdots \\ \theta_n \end{bmatrix}(size:(n+1)*1),\\ y=& \begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ \ y_m \end{bmatrix}(size:m*1) \end{align}\]要求$J(\theta)$的最小值,可以另$\frac{\partial}{\partial{\theta}}{J(\theta)}=0 \Rightarrow X^T(X\theta-y)=0$。所以:
\[\theta =(X^TX)^{-1}X^Ty\]两种方法的差异
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率$\alpha$ | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量$n$大时也能较好适用 | 需要计算 $(X^TX)^{-1}$如果特征数量$n$较大则运算代价大,因为矩阵逆的计算时间复杂度为$O(n^3)$,通常来说当$n$小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
逻辑回归
逻辑回归一般应用在分类问题中,通过引入逻辑函数(logistic function)$g(z)=\frac{1}{1-e^z}$,使得逻辑回归模型的假设函数$h_{\theta}(x)=g(\theta^Tx)$输出在$[0,1]$之间。$h(\theta)$的作用是,对于输入标量$x$,根据给定参数$\theta$输出$y=1$的可能性,即$h_{\theta}(x)=P(y=1|x;\theta)$。
重新定义代价函数: $J(\theta)=\frac{1}{m}Cost(h_{\theta}(x),y)$,对于线性回归:$Cost(h_{\theta}(x),y)=\sum_{j=1}^m\frac{1}{2}(h_{\theta}(x^i)-y^j)^2$;定义逻辑回归中:
\[Cost(h_{\theta}(x),y)= \begin{cases} -log(h_{\theta}(x)), & \text{if $y=1$}\\ -log(1-h_{\theta}(x)), & \text{if $y$=0} \end{cases}\]$h_{\theta}(x)$与$Cost(h_{\theta}(x),y)$之间的关系如图:
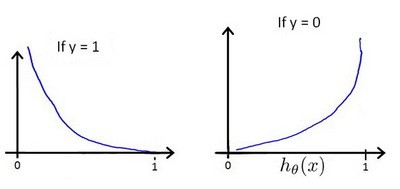
简化为: \(Cost(h_{\theta}(x),y)=-[y*log(h_{\theta}(x))+(1-y)*log(1-h_{\theta}(x))]\),从而:$Cost(h_{\theta}(x),y)=-[y*log(h_{\theta}(x))+(1-y) \times log(1-h_{\theta}(x))]$
\[J(\theta)=\frac{1}{m}\sum_{i=1}^m-[y^i*log(h_{\theta}(x^i))+(1-y^i)*log(1-h_{\theta}(x^i))]\]与线性回归相同,可以采用梯度下降法来求得最优参数:
\[\begin{align} repeat :&\\ &\theta_j := \theta_j-\alpha\frac{\partial}{\partial{\theta_j}}{J(\theta)},\ (j=0,1,...,m)\\ \end{align}\]其中,$\frac{\partial}{\partial{\theta_j}}{J(\theta)} = \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^i)-y^i)x_j^i$。
这里,似乎逻辑回归与线性回归算法是相同的,然而实际上由于二者的假设函数不同,所以逻辑回归的梯度下降与线性回归的梯度下降是两种不同的算法。
过拟合问题
解决方案:
- 丢弃一些不能帮助我们正确预测的特征。手工或者算法选择;
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
正则化线性回归
正则化线性回归的代价函数为:
由于未对$\theta_0$进行正则化,所以梯度下降算法将分两种情形:
\[\begin{align} repeat :&\\ & \theta_0 := \theta_0-\alpha \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^i)-y^i)x_0^i \\ &\theta_j := \theta_j-\alpha [\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^i)-y^i)x_j^i+\frac{\lambda}{m}\theta_j],\ (j=1,...,m)\\ \end{align}\]对上面$j=1,…,m$时的式子整理:$\theta_j=\theta_j(1-\alpha\frac{\lambda}{m}) - \frac{\alpha}{m}\sum_{i=1}^m[h_{\theta}(x^i)-y^i]x^i_j$,可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令$\theta$值减少了一个额外的值。
也可以利用正规方程求解:
\[\theta =(X^TX+\lambda \begin{bmatrix} 0 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{bmatrix})^{-1}X^Ty, \ \text{矩阵大小:(n+1)*(n+1)}\]正则化逻辑回归
正则化逻辑回归的代价函数为:
梯度下降算法:
\[\begin{align} repeat :&\\ & \theta_0 := \theta_0-\alpha \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^i)-y^i)x_0^i \\ &\theta_j := \theta_j-\alpha [\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^i)-y^i)x_j^i+\frac{\lambda}{m}\theta_j],\ (j=1,...,m)\\ \end{align}\]处理梯度下降法外,还有共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)等高级算法来求解最优参数,在matlab或octave中可以直接应用这些方法。